Acoustic Tape Measure
The Acoustic Tape Measure (Distance) program determines the physical distance between two XOs by measuring how long it takes sound pulses to travel between them.
I investigated the algorithm used by the Distance program to determine the feasibility of implementing it on the Lego NXT brick.
Program in Action
To start this activity, I first connected both XOs to the same shared network. Then I launched the Distance program on one XO by clicking the dolphin icon on the activity taskbar. The program sent an invitation to all neighboring computers, and from the second XO I clicked on the invitation from the Neighborhood view. At this point, “Begin Measuring Distance” buttons were activated on both XOs.
In the following video (with sound), we see the program in action. The XOs were placed relatively close to each other for the purpose of this video, but they perform reasonably well up to 10 meters apart.
When the XOs were not facing each other, however, the measurements were inaccurate. Although both XOs displayed synchronized readings, those readings fluctuated greatly, as we can see in the following video.
Algorithm
The Acoustic Tape Measure algorithm uses the fact that the XO’s microphone can hear the output of the XO’s own speaker. The algorithm works by turning on the microphones of both XOs and then having both XOs play distinctive sounds. One XO hears its own sound almost immediately, but there is a propagation delay before it hears the sound from the other XO. The XO that plays second hears the first XO’s sound delayed and hears its own sound immediately. Therefore, the first XO measures a longer interval between the two sounds, and the second XO measures a shorter interval. The difference between these measurements is twice the propagation delay, and combining this information with the approximated speed of sound, the XOs can determine their distance apart.
A more visual explanation is given below. The following diagram shows the interaction of the activities with respect to time.
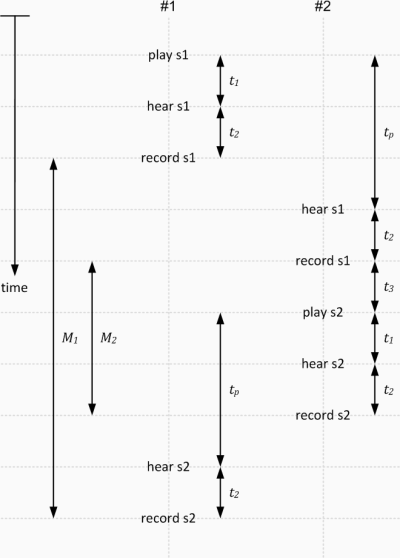
| Symbol | Description |
|---|---|
| M1 | The interval between recording s1 and s2 on computer #1. |
| M2 | The interval between recording s1 and s2 on computer #2. |
| tp | The propagation delay due to the distance of the two computers. |
| t1 | The interval between playing a sound and hearing the sound on the same computer. |
| t2 | The interval between hearing a sound and recording the sound. |
| t3 | The interval between recording a sound and playing a sound on computer #2. |
From the diagram, it is clear we can express M1 with tp, t1, t2 and t3.
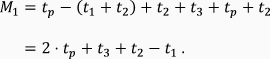
The relevant time intervals in the diagram are shown in red.
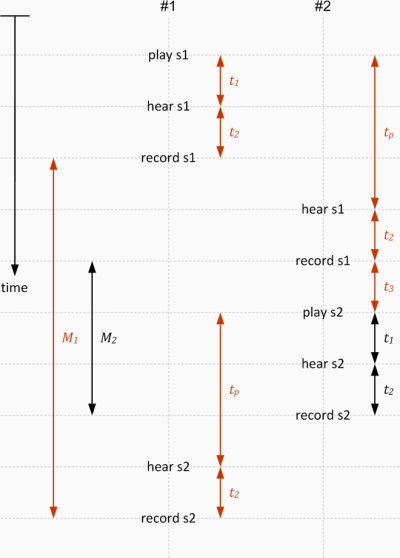
Similarly, we could express M2 with t1, t2 and t3.
![]()
The relevant time intervals in the diagram are shown in green.
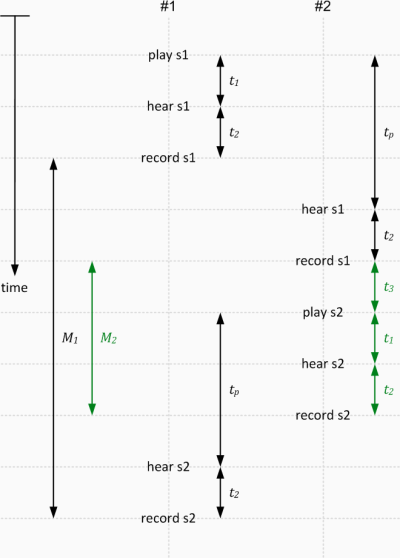
Therefore, we have the following relationship.
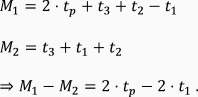
Since we assumed that an XO hears its own sound almost immediately, we can approximate t1 as zero and rewrite the equation as below, where d denotes the distance and csound denotes the speed of sound, which in 20 °C, dry air is 343 m/s.
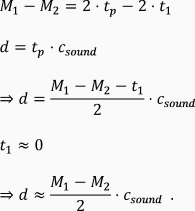
Assumptions
Note that we can assume t1 and t2 are the same on both computers because the two computers have exactly the same hardware capabilities. In other words, this algorithm works only if both computers have identical hardware.