NXT Distance Implementation
I studied the algorithm of the Acoustic Tape Measure (Distance) program for the OLPC XO. I also explored the possibilities of implementing this algorithm on the Lego NXT brick. I then implemented this algorithm as an autonomous program running on two NXT bricks. Source code is available in the last section of this page.
Implementation
I implemented the following state machines for the client unit (initiator) and the server unit (responder). The application starts by allowing the user to specify the NXT’s mode of operation, client or server, by pressing the left or right arrow buttons. The two NXTs then execute their state machines and continuously display synchronized distance results until user presses the escape button.
Client State Machine
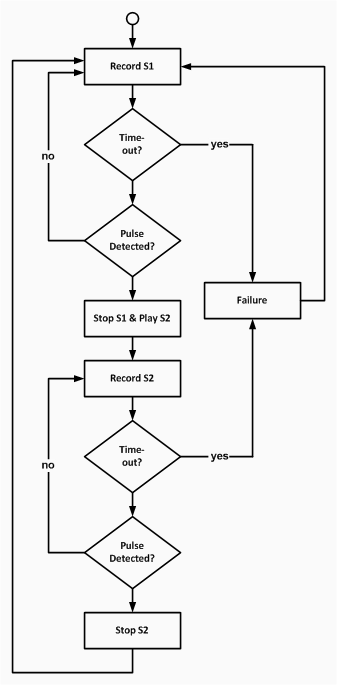
After the client initiates the connection with the server, it enters the following state machine. It starts by playing a tone (Play S1) and immediately recording the tone (Record S1). After waiting for the tone to finish playing (Stop S1), it waits for a tone from the server (Record S2). After it receives the second tone, it sends the timing M1 to the server and then receives the distance d from the server. It displays the distance and then waits a while (Stop S2) before playing another sound (Play S1).
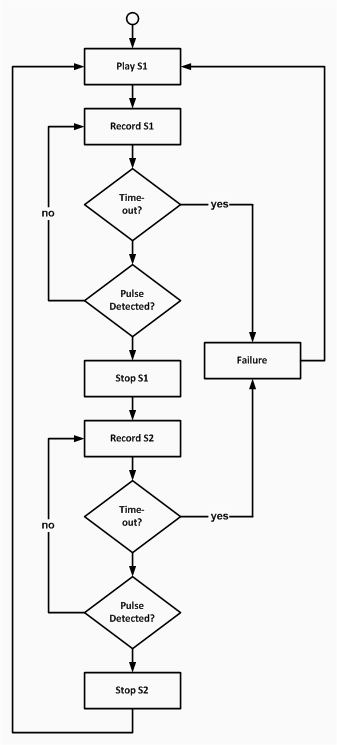
Server State Machine
After the server accepts a connection from the client, it enters the following state machine. It starts by recording a tone played by the client (Record S1). After waiting for the tone to finish playing, it starts to play a tone (Stop S1 and Play S2) and immediately records the second tone (Record S2). After receiving the timing M1 from the client, it calculates the distance d and sends it to the client. It displays this distance and then waits a while (Stop S2) before recording another sound (Record S1).
Event Timeline
In the ideal scenario, the timeline of events would be exactly as previously discussed. In real applications, however, there is a need to handle errors. For instance, the program needs to recover from missed recordings.
The following diagram shows the timeline for ideal cases in which when both parties detect sounds from each other. There are two complete cycles shown in the diagram, where p represents the time between two consecutive sound pulses. This time corresponds to interval between the rising edges of the pulses, and it is several times longer than then length of an individual pulse.
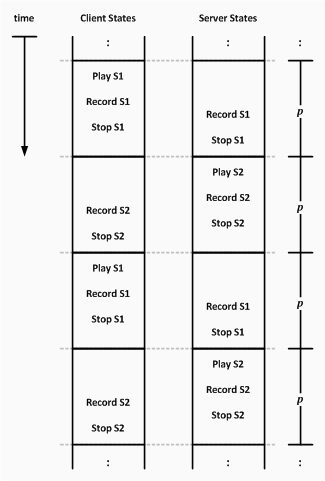
The application enters a failure state any time it fails to detect an expected sound pulse. It recovers from this condition, displays a failure message, and then enters the next measurement cycle normally. The following diagram shows the timeline when this occurs.

Program in Action
Both the client and server NXTs run the same version of the program, and the user must select which state machine they execute. After the client initiates the connection, the two NXTs take turns playing tones, and they display synchronized measurements. The program terminates when the user presses the escape button. If only one participant is left running, it will continue to function, but it will continuously display failures.
Just like the XO computers, it is best to position the NXTs so their speakers and microphones face each other. Otherwise the distance measurements are inaccurate. In the following video (with sound), I did not do this because I wanted to show both screens simultaneously in order to demonstrate how they display synchronized results.
The following video (with sound) demonstrates what occurs when two NXTs fail to detect sounds from the other participant. The NXTs continue to function after displaying a failure.
The following video (with sound) demonstrates the procedure I performed to generate readings for the charts in the next section.
Program Results
As discussed in the Distance algorithm and NXT sound system pages, there are some hardware limitations. In order the generate consistent readings, the NXTs must be in a quiet environment, away from walls, without obstacles between them, and without physical disturbances.
Recordings were computed using the following formula, where csound is 1.366×10-5 inches per nanosecond, corresponding to 347 meters per second, which is the speed of sound in 80 °F.
![]()
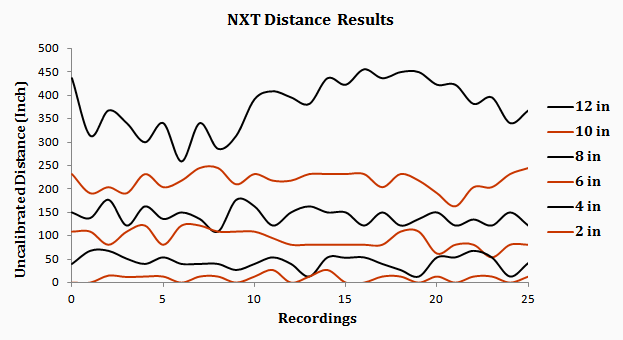
The following chart shows recorded distance versus actual distance for 6 different distances: 2 inches, 4 inches, 6 inches, 8 inches, 10 inches, and 12 inches. For each distance, 25 continuous recordings were used as data for the chart.
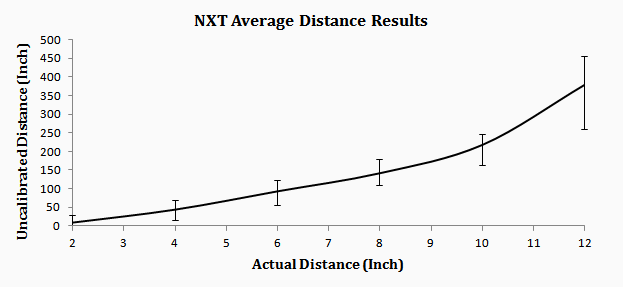
The following chart shows average recorded distance versus actual distance.
Analysis
The NXTs do not calculate the correct distances, but the values they calculate are consistent and do directly correspond to the actual distances of separation. It would be possible to simply factor the numbers by a constant, such as 20, to provide a more realistic reading.
Recall the two assumptions of the Distance algorithm: t1 equals zero, and the four durations of t2 in the event timeline are the same. The implementation must satisfy these conditions. On the NXT the speaker and sound sensor are in close proximity, so basic physics tells us that t1 is approximatly zero. To satisfy the second condition, I carefully constructed the code so that t2 was calculated using identical bits of code, i.e. a single method. In other words, all four different sound recording states of the two different state machines recorded sounds in identical ways.
In spite of this, there is clearly a discrepancy between the actual distances and the recorded distances. To investigate this problem, I performed two additional experiments on the NXTs.
The following chart shows the results of my first experiment. I programed an NXT as a sound generator and receiver. I had it play a fixed tone at different durations: 1/2 second, 1/20 second, and 1/200 second.
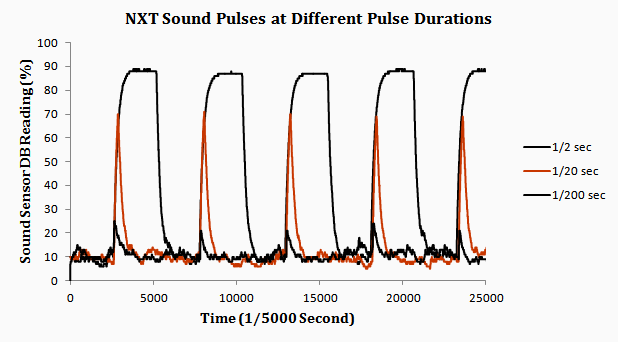
From this experiment, I learned that short sound durations would not suffice for the NXT Distance program. This is due to the fact that the attack time of the sound pluses is long, and a short duration, such as 1/20 second (50 millisecond), is not enough time for the sensor to detect a tone generated by another NXT at its peak volume.
For relatively long attack times, the time to reach the DB threshold did not seem consistent, it that could greatly affect the distance measurement. To study this further, I performed a second experiment. I programed one NXT as a sound pulse generator and a second NXT as a sound receiver. I played a fixed tone at a fixed duration at different distances: 2 inches, 6 inches, 10 inches, and 12 inches.
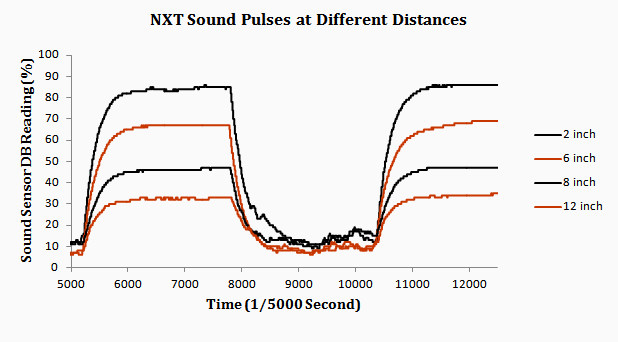
This experiment demonstrated that it would take significantly different periods of time to reach the DB threshold, based solely on the distance of separation between the two NXTs.
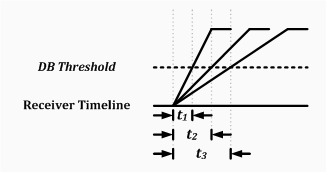
| Symbol | Description |
|---|---|
| t1 | The amount of time to reach the DB threshold for a sound pulse generated at a close distance. |
| t2 | The amount of time to reach the DB threshold for a sound pulse generated at an average distance. |
| t3 | The amount of time to reach the DB threshold for a sound pulse generated at a far distance. |
What I have found is the interval between two sound pulses measurements, M1 - M2, is in fact greater than 2 * tp, which was the original conclusion. The new formula is shown below, where td is delay caused by different attack times.
![]()
The following diagram demonstrates the origin of this new term:
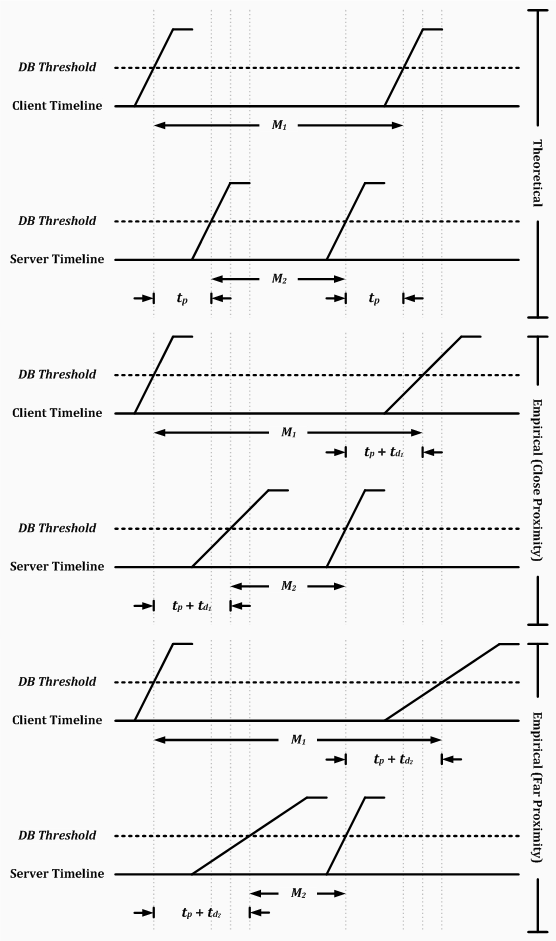
| Symbol | Description |
|---|---|
| M1 | The interval between recording sound 1 (s1) and sound 2 (s2) on the client. |
| M2 | The interval between recording s1 and s2 on server. |
| tp | The propagation delay due to the distance between the two computers. |
| td1 | The delay caused by different attack times at distance d1. |
| td2 | The delay caused by different attack times at distance d2. |
As we discussed previously, the usefulness of this algorithm is mainly restricted by the quick diminishing of sound sensitivity as the distance increases. NXT sound sensors are incapable of detecting sounds from other NXTs that are located only a couple of feet away. In the experiments above, the maximum distance shown was 12 inches, which is about as far away as it is possible to record accurate distances. Extremely quiet environments would allow the NXTs to distinguish sounds with greater sensitivity, but it is unlikely this would improve the performance dramatically.